
Riddle:
While playing with a metal washer shaped like a ring, Dave accidentally pushed it on his finger too far and couldn't get it off. Trying to remove it using soap and water didn't work. The hospital sent him to a service station thinking they could cut the metal. Since the ring was made with specially hardened steel, it couldn't be cut. Just then Bob arrived on the scene and suggested an easy way to remove the washer in just a few minutes. What was his solution?
Answer: Bob suggested that Dave hold his finger in the air while someone wound a piece of string tightly around his finger just above the metal ring. The string forced the swelling down. As they unwounded the string from the end nearest the ring, someone else slid the ring up. They continued winding and unwinding the string until the ring could be easily removed.
Riddle:
Two grandmothers, with their two granddaughters; Two husbands, with their two wives; Two fathers, with their two daughters; Two mothers, with their two sons; Two maidens, with their two mothers; Two sisters, with their two brothers; Yet only six in all lie buried here; All born legitimate, from incest clear. How can this be?
Answer: Two widows each had a son, and each widow married the son of the other and then each had a daughter.
Riddle:
A hunter met two shepherds, one of whom had three loaves and the other, five loaves. All the loaves were the same size. The three men agreed to share the eight loaves equally between them. After they had eaten, the hunter gave the shepherds eight bronze coins as payment for his meal. How should the two shepherds fairly divide this money?
Answer: The shepherd who had three loaves should get one coin and the shepherd who had five loaves should get seven coins. If there were eight loaves and three men, each man ate two and two-thirds loaves. So the first shepherd gave the hunter one-third of a loaf and the second shepherd gave the hunter two and one-third loaves. The shepherd who gave one-third of a loaf should get one coin and the one who gave seven-thirds of a loaf should get seven coins.
Riddle:
You want to send a valuable object to a friend. You have a box which is more than large enough to contain the object. You have several locks with keys. The box has a locking ring which is more than large enough to have a lock attached. But your friend does not have the key to any lock that you have. How do you do it? Note that you cannot send a key in an unlocked box, since it might be copied.
Answer: Attach a lock to the ring. Send it to her. She attaches her own lock and sends it back. You remove your lock and send it back to her. She removes her lock.
Riddle:
You go to the doctor because you're ill and he prescribes you with 3 pills and tells you to take them every half hour.
How long do the pills last you?
Answer: An hour because the first pill doesn't take 30 min. to take.
Riddle:
There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person. Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6, ...). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9, ...). This continues until all 100 people have passed through the room. What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?
Answer: First think who will operate each bulb, obviously person #2 will do all the even numbers, and say person #10 will operate all the bulbs that end in a zero. So who would operate for example bulb 48: Persons numbered: 1 & 48, 2 & 24, 3 & 16, 4 & 12, 6 & 8 ........ That is all the factors (numbers by which 48 is divisible) will be in pairs. This means that for every person who switches a bulb on there will be someone to switch it off. This willl result in the bulb being back at it's original state. So why aren't all the bulbs off? Think of bulb 36:- The factors are: 1 & 36, 2 & 13, 6 & 6 Well in this case whilst all the factors are in pairs the number 6 is paired with it's self. Clearly the sixth person will only flick the bulb once and so the pairs don't cancel. This is true of all the square numbers. There are 10 square numbers between 1 and 100 (1, 4, 9, 16, 25, 36, 49, 64, 81 & 100) hence 10 bulbs remain on.
Riddle:
You are given a set of scales and 12 marbles. The scales are of the old balance variety. That is, a small dish hangs from each end of a rod that is balanced in the middle. The device enables you to conclude either that the contents of the dishes weigh the same or that the dish that falls lower has heavier contents than the other. The 12 marbles appear to be identical. In fact, 11 of them are identical, and one is of different weight. Your task is to identify the unusual marble and discard it. You are allowed to use the scales three times if you wish, but no more. Note that the unusual marble may be heavier or lighter than the others. How can you identify it and determine whether it is heavy or light?
Answer: Number the marbles from 1 to 12. For the first weighing put marbles 1,2,3 and 4 on one side and marbles 5,6,7 and 8 on the other. The marbles will either they balance or not. If they balance, then the different marble is in group 9,10,11,12. Thus, we would put 1 and 2 on one side and 9 and 10 on the other. If these balance then the different marble is either 11 or 12. Weigh marble 1 against 11. If they balance, the different marble is number 12. If they do not balance, then 11 is the different marble. If 1 and 2 vs 9 and 10 do not balance, then the different marble is either 9 or 10. Again, weigh 1 against 9. If they balance, the different marble is number 10, otherwise, it is number 9. That was the easy part. What if the first weighing 1,2,3,4 vs 5,6,7,8 does not balance? Then any one of these marbles could be a different marble. Now, in order to proceed, keep track of which side is heavy for each of the following weighings. Suppose that 5,6,7 and 8 is the heavy side. We now weigh 1,5 and 6 against 2,7 and 8. If they balance, then the different marble is either 3 or 4. Weigh 4 against 9, a known good marble. If they balance then the different marble is 3 or 4. Then, if 1,5 and 6 vs 2,7 and 8 do not balance, and 2,7,8 is the heavy side, then either 7 or 8 is a different, heavy marble, or 1 is a different, light marble. For the third weighing, weigh 7 against 8. Whichever side is heavy is the different marble. If they balance, then 1 is the different marble. Should the weighing of 1,5 and 6 vs 2,7 and 8 show 1,5,6 to be the heavy side, then either 5 or 6 is a different heavy marble or 2 is a light different marble. Weigh 5 against 6. The heavier one is the different marble. If they balance, then 2 is a different light marble.
Riddle:
If it is 1,800 kilometers to America, 1,200 kilometers to Japan, 2,400 kilometers to New Zealand, and 1,400 kilometers to Brazil-
How far is Morocco?
Answer: The answer is 1,700 kilometers, as vowels in the countries' names are worth 300 kilometers and the consonats are worth 200 kilometers.
Riddle:
I like indigo but not blue, I like onions but not turnips, I like forms but not shapes. According to the same rule, do I like tomatoes or avocados?
Answer: Avocadoes - I like all things that start with a preposition.
Riddle:
There are three guards and three prisoners who need to cross a river. Their boat only holds two people at a time, and the number of prisoners must NEVER be allowed to outnumber the number of guards on either side of the river; otherwise, the prisoners will overpower the guards and, well, the story will come to an abrupt end. List each of the trips that need to be made and who is in the boat, and who is on each of the riverbanks during each trip. How many trips it will take to safely transport all of the guards and prisoners across the river?
Answer: The riddle requires three trips to complete the task!
First trip: G1 and G2 (guard #1 and guard #2) cross the riverSecond trip: P1 (Prisoner #1) and G3 (guard #3) cross the riverThird trip: G1, G2, P2 (Prisoner #2), and P3 (Prisoner #3) cross the river
Riddle:
How can this be true? Have a look at the picture. All the lines are straight, the shapes that make up the top picture are the same as the ones in the bottom picture so where does the gap come from?
Answer: The green triangle has dimensions 2 x 5 and gradient 2 / 5 = 0.4 The red triangle has dimensions 3 x 8 and gradient 3 / 8 = 0.375 Hence the gradient of the green triangle is greater than that of the red triangle.
Riddle:
A man enters an expensive restaurant and orders a meal. When the waiter brings him his meal the man takes out a slip of paper and writes down 102004180, then leaves. The cashier hands the slip of paper to the cashier who understood it immediately.
What did the slip of paper say?
Answer: I =1, 0=Ought, 2=To, 0=Owe, 0=Nothing, 4=For, 1=I, 8=Ate, 0=Nothing. I Ought To Owe Nothing For I Ate Nothing. 102004180
Riddle:
You are locked in a house and you have four objects. You have a wooden chair, a ladder, a piano, and a rubber ax. You can only pick one object and you can't get out by breaking anything. What would you use to get out?
Answer: You use the piano KEYS to ulock the door!
Riddle:
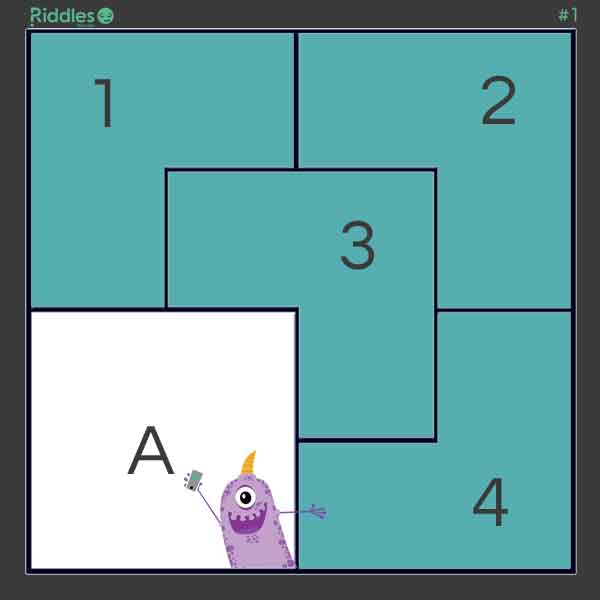
Carl is trying to find solutions to a geometric puzzle. He has a square plot of land that he needs to reserve 1/4 for himself and divide the remaining 3/4 equally and in a similar shape, among his 4 children. There are two possible solutions. Can you solve the puzzle?
Answer: Solution #1 - Squares
First, Carl divides his as to reserve to himself one-fourth in the form of a square.
 Then, Carl takes the remaining 3/4 shape and scales it down by 1/4. He then, multiplies the shape into 4 identically shaped pieces, and aranges them so that they fit into the original 3/4 shape.
Then, Carl takes the remaining 3/4 shape and scales it down by 1/4. He then, multiplies the shape into 4 identically shaped pieces, and aranges them so that they fit into the original 3/4 shape.
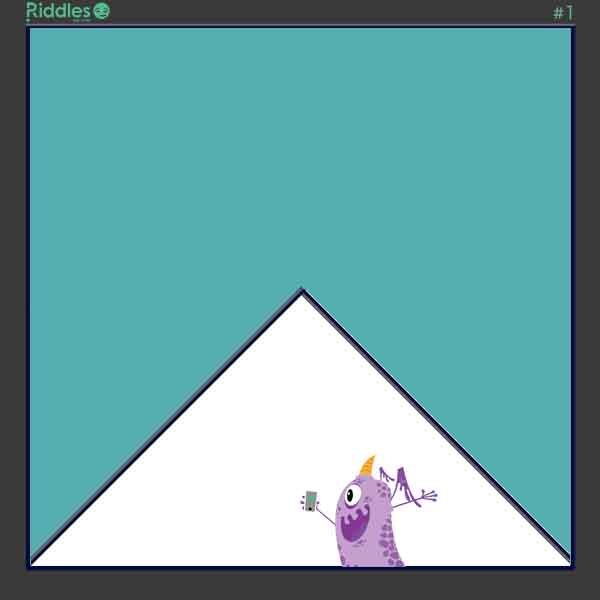
 Solution #2 - Rectangles
First, create a triangle that is 1/4 the size of the square.
Solution #2 - Rectangles
First, create a triangle that is 1/4 the size of the square.
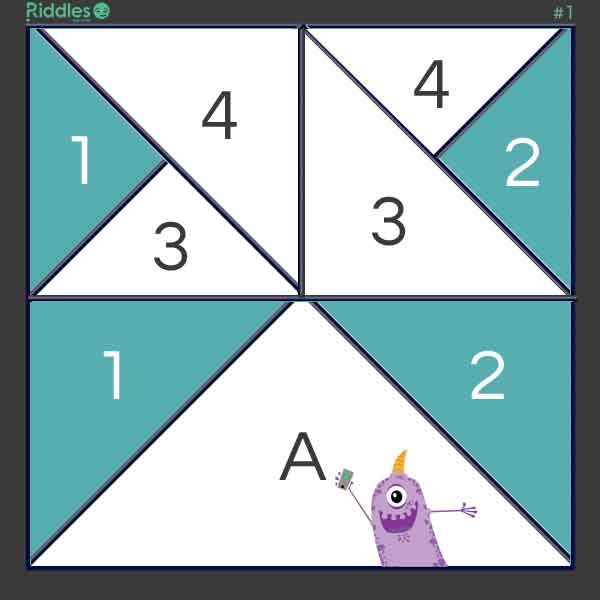
 Now, with straight lines, create two squares.
Proceed to disect the two squares with horizontal lines creating 4 triangles.
Then, disect one of the resultuing triangles from each square. The shape of land for each of his four children is divided evenly and is the same shape.
Now, with straight lines, create two squares.
Proceed to disect the two squares with horizontal lines creating 4 triangles.
Then, disect one of the resultuing triangles from each square. The shape of land for each of his four children is divided evenly and is the same shape.
 Then, Carl takes the remaining 3/4 shape and scales it down by 1/4. He then, multiplies the shape into 4 identically shaped pieces, and aranges them so that they fit into the original 3/4 shape.
Then, Carl takes the remaining 3/4 shape and scales it down by 1/4. He then, multiplies the shape into 4 identically shaped pieces, and aranges them so that they fit into the original 3/4 shape.
 Solution #2 - Rectangles
First, create a triangle that is 1/4 the size of the square.
Solution #2 - Rectangles
First, create a triangle that is 1/4 the size of the square.
 Now, with straight lines, create two squares.
Proceed to disect the two squares with horizontal lines creating 4 triangles.
Then, disect one of the resultuing triangles from each square. The shape of land for each of his four children is divided evenly and is the same shape.
Now, with straight lines, create two squares.
Proceed to disect the two squares with horizontal lines creating 4 triangles.
Then, disect one of the resultuing triangles from each square. The shape of land for each of his four children is divided evenly and is the same shape.

Riddle:
Angry and Hungry are two words ending in 'gry" There are three words, (Using popular terminology) in the English Language, that ends in "GRY".
The word is something that everyone uses every day. If you have listened carefully, I have already told you what it is. What is the third word?
Answer: The answer is terminology. It's the third word ending in gry. Using popular terminology
Riddle:
Three working women have different careers. If only one of statements 1, 2 and 3 are true, can you tell whether or not Mary is a nurse? 1. This statement is only true if statement 5 is false. 2. This statement is true if statements 4 or 5, or both 4 and 5 are true. 3. This statement is false only if both statements 6 and 1 are true. 4. Mary is a nurse 5. Karen is an artist. 6. Sarah is a photographer.
Answer: Mary is not a nurse. The way to solve this riddle is to consider statements 4, 5, and 6 and create a chart of all possible true and false answers. Next, fill in the chart according to statements 1 through 3. You will discover that there is only one line where only one of the statements one, two, and three are true. Thus, it is determined that: Statements 4 and 5 are false and statement 6 is true.
Riddle:
A man told his son that he would give him $1000 if he could accomplish the following task. The father gave his son ten envelopes and a thousand dollars, all in one dollar bills. He told his son, "Place the money in the envelopes in such a manner that no matter what number of dollars I ask for, you can give me one or more of the envelopes, containing the exact amount I asked for without having to open any of the envelopes. If you can do this, you will keep the $1000." When the father asked for a sum of money, the son was able to give him envelopes containing the exact amount of money asked for. How did the son distribute the money among the ten envelopes?
Answer: The contents or the ten envelopes (in dollar bills) should be as follows: $1, $2, $4, $8, $16, $32, $64, $128, $256, $489. The first nine numbers are in geometrical progression, and their sum, deducted from $1,000, gives the contents of the tenth envelope.
Answer explained: The son distributed $1000 into ten envelopes using a clever binary-like approach to ensure he could provide any exact amount from $1 to $1000 by handing over a combination of envelopes without opening them. The first nine envelopes contain amounts that are powers of 2: $1, $2, $4, $8, $16, $32, $64, $128, and $256$, which total $511. The tenth envelope holds the remaining $489 ($1000 - $511$).This setup works because the first nine envelopes can form any amount up to $511 through unique combinations, much like binary numbers. For amounts between $489 and $1000, the son uses the $489 envelope plus a combination of the first nine envelopes to cover the difference—for example, $512 = $489 + $23$, where $23 is made from $16 + $4 + $2 + $1$. This ensures every possible amount from $1 to $1000 can be achieved with a unique combination of envelopes.
Answer explained: The son distributed $1000 into ten envelopes using a clever binary-like approach to ensure he could provide any exact amount from $1 to $1000 by handing over a combination of envelopes without opening them. The first nine envelopes contain amounts that are powers of 2: $1, $2, $4, $8, $16, $32, $64, $128, and $256$, which total $511. The tenth envelope holds the remaining $489 ($1000 - $511$).This setup works because the first nine envelopes can form any amount up to $511 through unique combinations, much like binary numbers. For amounts between $489 and $1000, the son uses the $489 envelope plus a combination of the first nine envelopes to cover the difference—for example, $512 = $489 + $23$, where $23 is made from $16 + $4 + $2 + $1$. This ensures every possible amount from $1 to $1000 can be achieved with a unique combination of envelopes.
Riddle:
How can the number four be half of five?
Answer: It's true if you think of Roman numerals. FIVE, take away the F and the E and you are left with IV, half of the word FIVE, which is the Roman number for Four.

